Skip to content

Q-LavHA

With the knowledge gained on topographic controls and modeling from the previous exercise, we will now look at Q-LavHA1 as an alternative approach for probabilistic hazard assessments for lava flow inundation. This part of the exercise assumes that you have already installed both QGIS and Q-LavHA. The Q-LavHA user manual contains some important information about how to configure the model and the data, so we encourage you to have a look at it at some point.

Objectives

  • Review the theory behind Q-LavHA.
  • Understand the main assumptions behind the use of the model.
  • Perform probabilistic lava flow modeling for several vents in La Palma.
  • Account for the uncertainty in vent locations in hazard assessments.

Theory behind Q-LavHA

Flow direction

The starting philosophy behind Q-LavHA is similar to the analysis performed for the path of steepest descent approach: using the DEM, the model will try to estimate where the flow will go next based on the maximum \(\Delta h\) of the surrounding pixels. However, Q-LavHA uses a probabilistic approach to estimate this flow direction.

Firstly, as we saw, a lava flow is a Non-Newtonian fluid with yield strength, which means that it can escape the steepest path and propagate laterally, fill depressions and overcome topographical obstacles. To account for that, Q-LavHA introduces 2 corrective factors:

  • \(H_c\), representing the flow thickness.
  • \(H_p\), representing the ability of a flow to inflate.

Together, these two parameters help avoiding the modelled flow getting stuck in topographic low and will allow it to spread laterally, as we saw the 2021 flow of La Palma was able to do.

Secondly, the initial estimation of path of steepest descent is performed stochastically similarly to what we previously looked at. Conceptually, one Q-LavHA output is constituted by the simulation of thousands of lava flows (1500 by default). Each lava flow simulation applies a path of steepest descent approach, but the selection of the next pixel is performed slightly differently:

  1. At each new pixel, the \(H_c\) and \(H_p\) corrections are applied to the active pixel according to Figure 1.
  2. Instead of selecting the pixel with the largest \(|\Delta h|\) as previously seen, Q-LavHA assigns a relative probability of flow inundation to each surrounding pixel (see box below).
  3. Using a random number generator, Q-LavHA stochastically sample which pixel will be inundated next. With this approach, the pixel with the largest \(|\Delta h|\) has the highest probability of being inundated next, but other pixel also have a non-null probability of inundation.
Path of steepest descent in Q-LavHA

By default, Q-LavHA computes a relative probability across the 8 surrounding pixels using \(\Delta h^2\) according to:

\[ P_i^2 = \frac{(\Delta h_i)^2}{\sum_{j=1}^{8} (\Delta h_i)^2}, i=1,2,\ldots,8 \]

If potential topographic obstacles are not overcome by the application of \(H_c\) and \(H_p\) around the 8 surrounding pixels, Q-LavHA extends its search to the next 16 surrounding pixels. Q-LavHA then transforms these relative probabilities into a cumulative probability function \(S_i\):

\[ S_i = \sum_{j=1}^{i} P_j, i=1,2,\ldots,8 \]

A random number \(rnd\) is then drawn in the \([0, 1[\) interval, and used to select the corresponding pixel in the range \([S_{i-1}, Si[\):

\[ S_{i-1} \leq rnd \leq S_i, i=1,2,\ldots,8 \]

pixel

Figure 1: Topographic corrections applied in `Q-LavHA`.

Flow length

Flow length is a critical metrics of lava flow hazard. However, since it depends on a complex interaction between eruption conditions at the source, flow rheology and topography through time and space, modelling the case-per-case physics of each flow is unrealistic in hazard assessment contexts. For this reason, Q-LavHA proposes three alternatives to compute maximum flow length:

  1. A maximum user defined length, using either Euclidean or Manhattan distances.
  2. A decreasing probability function based on existing flow databases.
  3. The cooling-limited flow model FLOWGO2.

Lava flow distance

As you can see from the geological map of La Palma, most historical flows on the island have reached the sea, so we will consider here that the flow distance is of limited importance. This assumption is however invalid in most cases. The probability function option allows you define a probability of flow length based on a mean and standard deviation of known lava flows length, which is a convenient way to treat this parameter probabilistically. Refer to the original paper1 for more information.

Probability of flow inundation

As previously seen, probability of lava flow inundation \(P\) at a given pixel \(x, y\) is generally computed as the number of inundation counts \(n_i\) normalised by the number of runs \(N_r\):

\[ P(x,y) = \frac{\sum_{i=1}^{N_{r}}n_{i}}{N_{r}} \]

Where \(N_{r}\) is the total number of runs and \(n_{i}\) is defined as:

\[ n_{i} = \bigg\{ ^{1,\ if\ inundation} _{0,\ otherwise} \]

Depending on the modeling options adopted, Q-LavHA will slightly modify this approach. Refer to the original paper1 for more information.

Exercise

Install Q-LavHA

Image title Start by making sure that Q-LavHA has been properly installed according to this guide. You should see this icon in the toolbar.

  • In the Lava Flow exercise layer group in QGIS, activate the Vents Exercise layer.

Running Q-LavHA for single vents

These vents correspond to those indicated in the Table below. Q-LavHA requires projected UTM coordinates, which are shown in the Easting and Northing columns (x and y columns, respectively). The UTM zone for La Palma is 28N, or EPSG:3268.

Vent Latitude Longitude Easting (m) Northing (m) EPSG
Vent 1 -17.83989 28.62507 222340 3169746 32628
Vent 2 -17.86626 28.61262 219728 3168426 32628
Vent 3 -17.84316 28.58782 221922 3165623 32628
Vent 4 -17.81585 28.60777 224646 3167772 32628
Vent 5 -17.84649 28.49699 221357 3155562 32628

Coordinate systems

Here, you are provided with input data that all have the same coordinate system. Before modeling lava flows for your own projects, make sure that you first reproject all your data to a unique CRS.

Model setup

Let's run Q-LavHA for each of the vents defined above. For now, we will assume that we know exactly the vent location. Open the Q-LavHA window, and let's look at the parameters:

  1. In the DEM Selection box, select the Data/Lava/DEM_Qlavah.tif. In the DEM selection window, make sure you change the type of files from .asc to .tif.
  2. As a Vent Type, choose Point for now.
  3. Add the relevant Coordinates.

  1. Lava Flow Propagation: This section sets up the behaviour of the lava flow, as described in the theory section.

    • Leave the default values of Hc and Ht.
    • Use the H16 option: This means that the algorithm will first search for a topographic low within the first 8 adjacent pixels, and will extend the search to the next 16 ones if not found.
    • Use Probability to the square

  2. Lava Flow Length Constrain: This section defines when a lava flow stops. You can switch between the various options for an illustration of the different behaviours. As discussed above, use a Manhattan Distance with a length of 10000 m.

  3. Simulations: Use a Number of iterations of 1500. This represents the number of simulated lava flows, or \(N_r\) in the equations above.
  1. Set an Output path and a name to the output layers.
  2. Save the Parameters.

You are now ready to run the simulation!

Vent geometry

Q-LavHA offers different source geometries, such as a fissure, or a vent opening susceptibility map. The choice of these options depends on the case study, and their use is described in the Q-LavHA user manual.

Styling outputs

Upon completion of the model run, the output file is directly added to the layer panel. Let's change its visualisation:

  • Open the Layer Properties panel by double-clicking on the output layer in the Layers panel.
  • From the Symbology tab on the left:
    • Under Color Rendering, uncheck the Colorize option.
    • Under Render type, choose Singleband pseudocolor.
    • Set the min and max values to 0 and 0.5, respectively.
    • Change the Color ramp to Magma
  • Click ok.

The output file now shows the spatial distribution of inundation probability varying between \(\gt 0\) and \(0.5\) (i.e., 50%).

Copying layer symbology

In QGIS, you can simply copy the display properties of one layer to other layers:

  • In the Layers panel, right-click on the layer you want to copy the style from and select Styles > Copy style.
  • Now right-click on the layer you want to apply to style on and select Styles > Paste style.

copy styles

Analysing results

Following this procedure, run Q-LavHA for all the vents specified in the Table above and apply the same symbology. Answer the following questions:

Question 1: Single-vent simulations

  1. How do modelled flows compare to historical lava flows in terms of length and width?
  2. Analyse and discuss the spatial distribution of inundation probability. How do they compare to flow accumulation rasters and the path of steepest descent approach?
  3. Where do branching occur?
  4. Chose one vent for which you will produce another run with the same parameters as above. Are they exactly the same? If not, why?
  5. Compare simulations from vent 2 with the flow outlines of the 2021 eruption. When and where is the model doing a good job? When and where is it not? Why?

Using several vents

Even in monogenetic vents, one eruptive episode can consist of multiple satellite vents. This was certainly the case for the 2021 eruption of La Palma. In fact, as you can see from the 2021 Vents layer in QGIS, CEMS identified that ~10 vents opened over a 500 x 500 m area. Here, we won't attempt predicting the number or the location of each vent; instead, we will model lava flow inundation from a grid of vents within a surface area and explore how vent location affects the lava flow simulation hazard.

(Not) one vent to rule them all

You've each been assigned one of the vents defined in the table above. Since this step takes more computational time, please run this procedure only for this vent.

Define the area

We will define a potential vent opening surface as a 500 x 500 m square centered on the reference coordinates of your attributed vent. Note that UTM coordinates are in meter: you can therefore simply identify the x and y coordinates these four points by addition and subtraction:

  • Lower left corner
  • Lower right corner
  • Upper right corner
  • Upper left corner

Model setup

  • From QGIS open Q-LavHA. Most of the parameters should already be filled. Otherwise, you can use the Load parameters option.
  • Set a Distance between vents of 100 m. Since we definerd a 500 x 500 m area, Q-LavHA will therefore model lava flow inundation from 25 vents.
  • Enter the 4 coordinates previously defined.
  • In the Lava Flow Parameter tab, change the Number of Simulations to 100. This will help save some computation time.
  • Make sure you change the output name.

Run the model!

Analysing results

Apply the same methodology to the surface area runs as you did for the point run.

Question 2: Vent location uncertainty

  1. Compare the run with its single-vent counterpart. How do they differ and why?

Prepare your hazard maps

The raw geotiff files produced by Q-LavHA are your main hazard files. If you choose to work in QGIS you can further export them to maps using the Print Layout tool (→ doc & tutorial).

Food for thoughts

Forecasting the flows from the 2021 eruption

Compare the Q-LavHA run with the flow outlines from the 2021 eruption below. Note that the Q-LavHA run was performed using the same 500 x 500 m source area as used above.

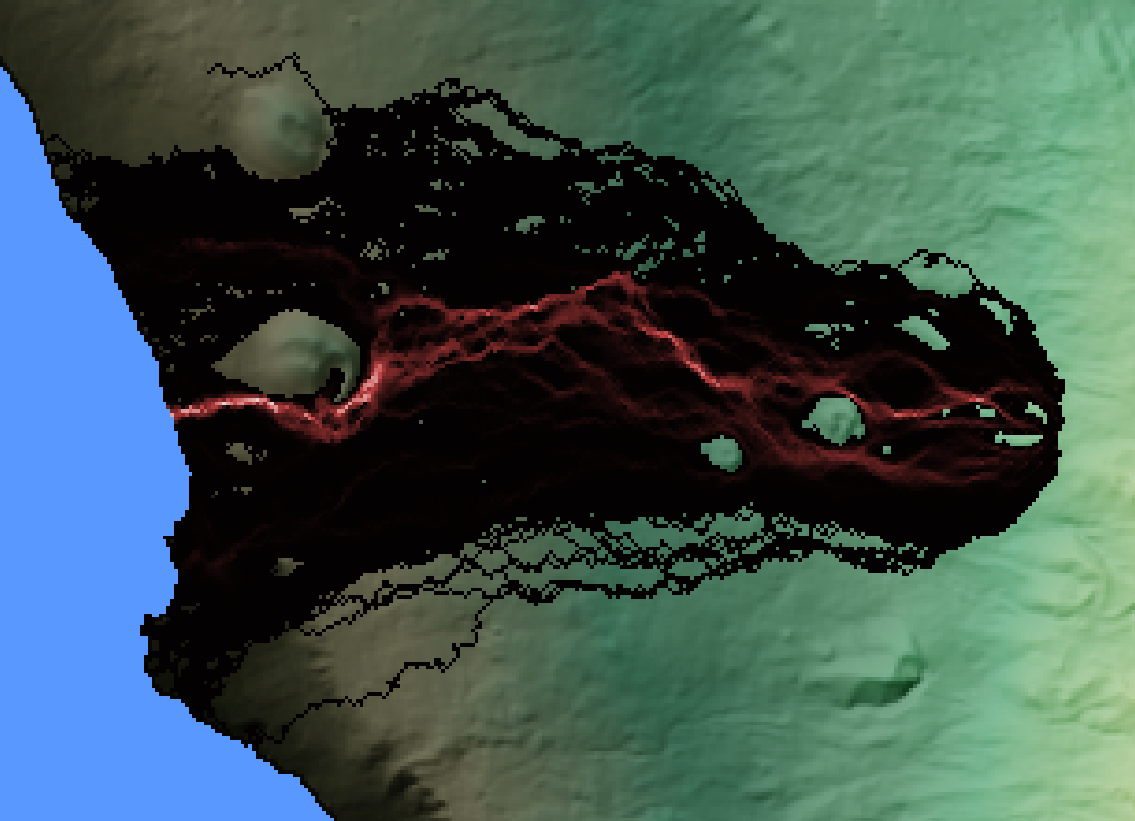
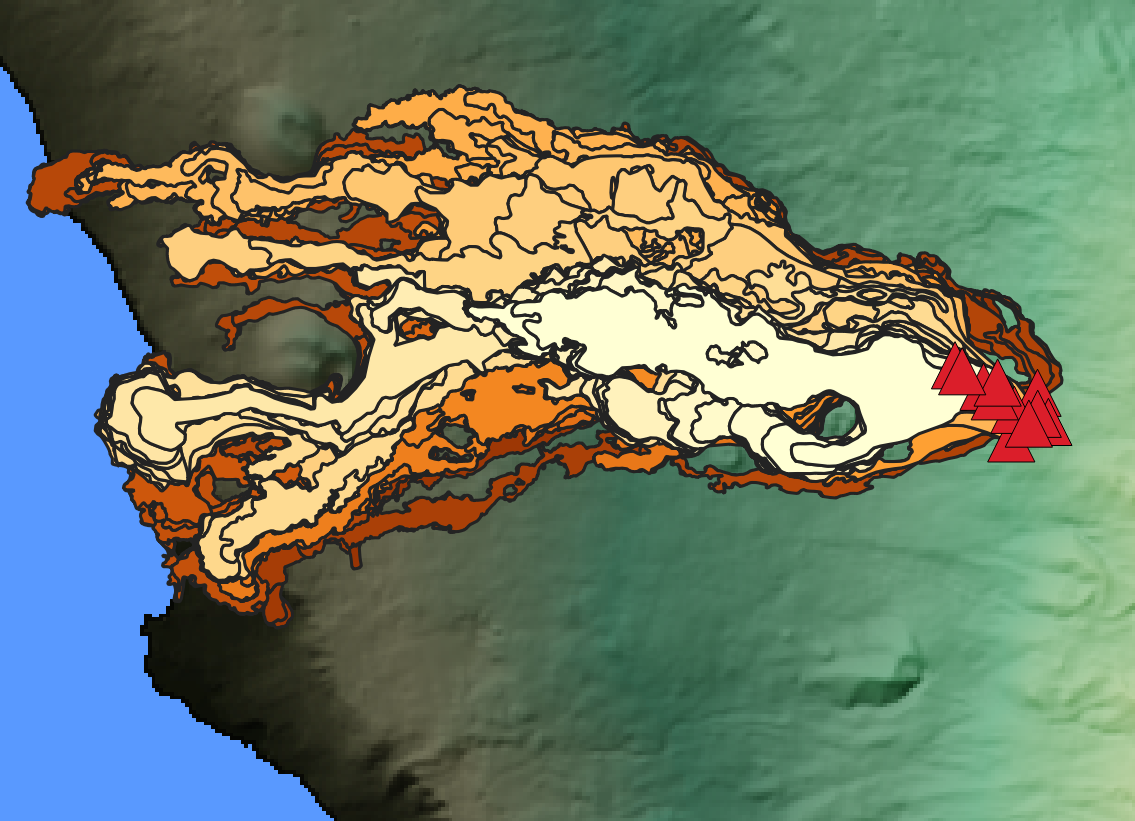
Q-LavHA2021

Q-LavHA2021

Question 3: Interpreting hazard forecasts

  1. From what you know about both the 2021 eruption and the dynamics of lava flows, compare and discuss the hazard forecast and the actual deposit. What are Q-LavHA's strengths and limitations?

Summary

In this exercise, you have:

  • Understood the philosophy behind a probabilistic model for lava flow inundation, Q-LavHA.
  • Assessed the hazard of lava flow inundation using probabilistic modeling.
  • Included the uncertainty on vent location in hazard estimates.
  • Understood the limitations of model predictions when compared to past events.

References

  1. Mossoux, S., Saey, M., Bartolini, S., Poppe, S., Canters, F., Kervyn, M., 2016. Q-LAVHA: A flexible GIS plugin to simulate lava flows. Computers & Geosciences 97, 98–109. https://doi.org/10.1016/j.cageo.2016.09.003 ↩↩↩

  2. Harris, A.J., Rowland, S. FLOWGO: a kinematic thermo-rheological model for lava flowing in a channel. Bull Volcanol 63, 20–44 (2001). https://doi.org/10.1007/s004450000120 ↩